What Game Theory Reveals About Life, The Universe, and Everything

This is about the most famous problem in game theory. Problems of this sort pop up everywhere, from nations locked in conflict to roommates doing the dishes. Even game shows have been based around this concept. Figuring out the best strategy can mean the difference between life and death, war and peace, flourishing and the destruction of the planet. And in the mechanics of this game, we may find the very source of one of the most unexpected phenomena in nature: cooperation.

On the 3rd of September, 1949, an American weather monitoring plane collected air samples over Japan. In those samples, they found traces of radioactive material. The Navy quickly collected and tested rainwater samples from their ships and bases all over the world. They also detected small amounts of Cerium-141 and Yttrium-91. But these isotopes have half-lives of one or two months, so they must have been produced recently and the only place they could have come from was a nuclear explosion.

But the US hadn't performed any tests that year, so the only possible conclusion was that the Soviet Union had figured out how to make a nuclear bomb. This was the news the Americans had been dreading. Their military supremacy achieved through the Manhattan Project was quickly fading. This makes the problem of Western Europe and the United States far more serious than it was before and perhaps makes the imminence of war greater. Some thought their best course of action was to launch an unprovoked nuclear strike against the Soviets while they were still ahead.

In the words of Navy Secretary Matthews to become "aggressors for peace". John von Neuman, the founder of game theory, said, "If you say why not bomb them tomorrow, I say, why not bomb them today? If you say today at five o'clock, I say why not at one o'clock?" Something needed to be done about nuclear weapons and fast. But what? In 1950, the RAND Corporation, a US-based think tank was studying this question. And as part of this research, they turned to game theory.

That same year, two mathematicians at RAND had invented a new game, one which unbeknownst to them at the time, closely resembled the US-Soviet conflict. This game is now known as the prisoner's dilemma. So let's play a game. A banker with a chest full of gold coins invites you and another player to play against each other. You each get two choices. You can cooperate or you can defect. If you both cooperate, you each get three coins. If one of you cooperates, but the other defects, then the one who defected gets five coins and the other gets nothing.

And if you both defect, then you each get a coin. The goal of the game is simple: to get as many coins as you can. So what would you do? Suppose your opponent cooperates, then you could also cooperate and get three coins or you could defect and get five coins, instead. So you are better off defecting, but what if your opponent defects, instead? Well, you could cooperate and get no coins or you could defect and at least get one coin.

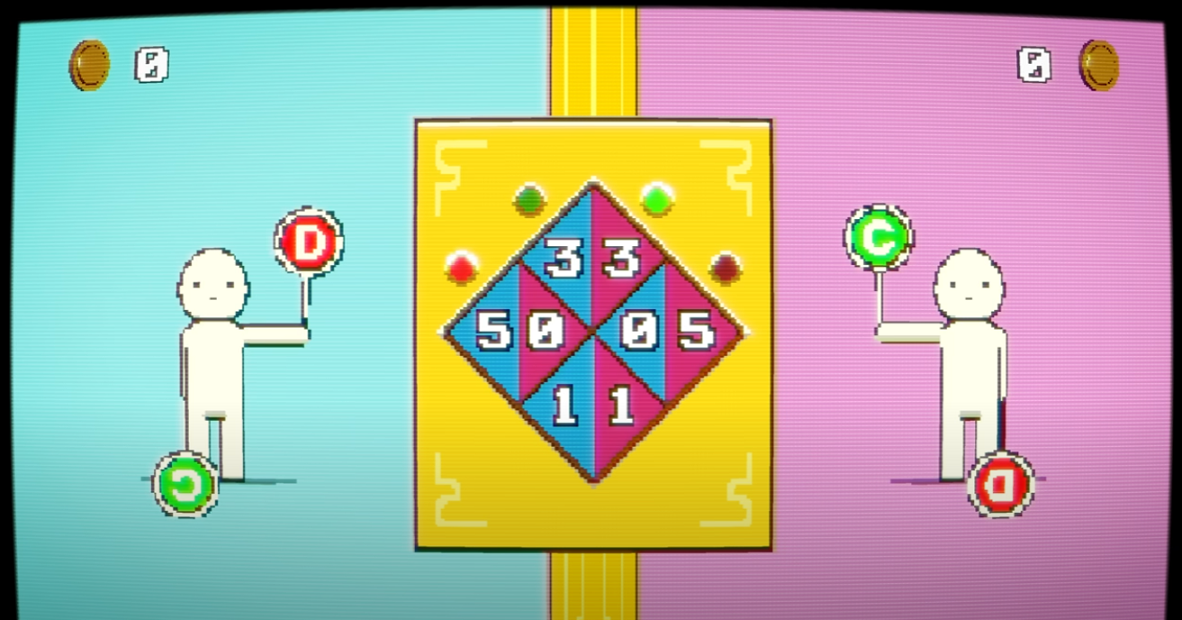
So no matter what your opponent does, your best option is always to defect. Now, if your opponent is also rational, they will reach the same conclusion and therefore also defect. As a result, when you both act rationally, you both end up in the suboptimal situation getting one coin each when you could have gotten three, instead. In the case of the US and Soviet Union, this led both countries to develop huge nuclear arsenals of tens of thousands of nuclear weapons each, more than enough to destroy each other many times over.

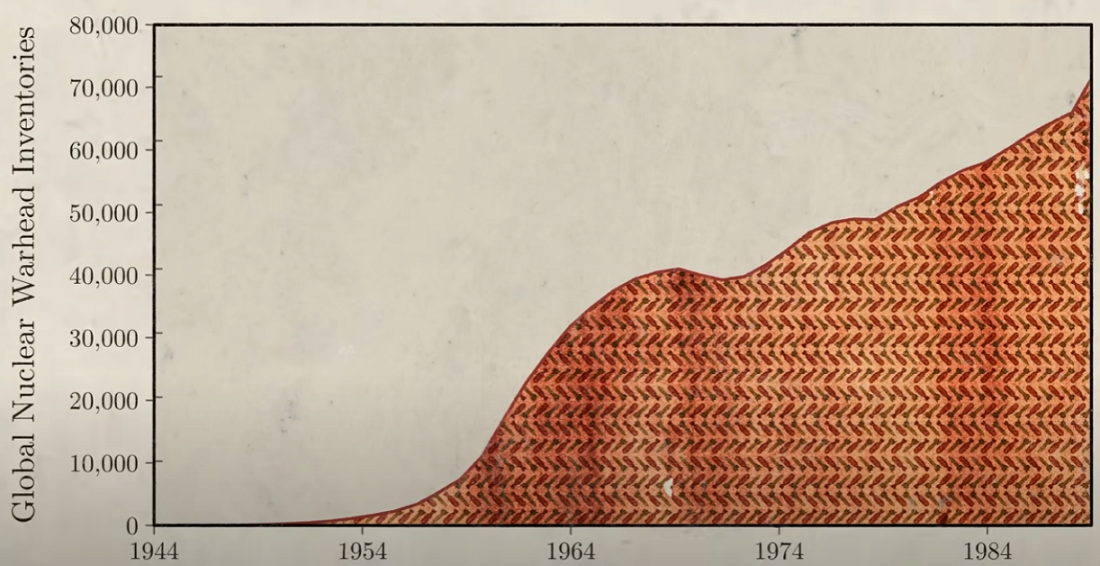
But since both countries had nukes, neither could use them. And both countries spent around $10 trillion developing these weapons. Both would've been better off if they had cooperated and agreed not to develop this technology further. But since they both acted in their own best interest, they ended up in a situation where everyone was worse off. The prisoner's dilemma is one of the most famous games in game theory. Thousands and thousands of papers have been published on versions of this game. In part, that's because it pops up everywhere.

Impalas living in between African woodlands and Savannahs are prone to catching ticks, which can lead to infectious diseases, paralysis, even death. So it's important for impalas to remove ticks and they do this by grooming, but they can't reach all the spots on their bodies and therefore they need another impala to groom them. Now, grooming someone else comes at a cost. It costs saliva, electrolytes, time and attention, all vital resources under the hot African sun where a predator could strike at any moment.

So for the other impala, it would be best not to pay this cost, but then again, it too will need help grooming. So all impalas face a choice: should they groom each other or not? In other words, should they cooperate or defect? Well, if they only interact once, then the rational solution is always to defect. That other impala is never gonna help you, so why bother? But the thing about a lot of problems is that they're not a single prisoner's dilemma.

Impalas see each other day after day and the same situation keeps happening over and over again. So that changes the problem because instead of playing the prisoner's dilemma just once, you're now playing it many, many times. And if I defect now, then my opponent will know that I'd defected and they can use that against me in the future. So what is the best strategy in this repeated game?

That is what Robert Axelrod, a political scientist wanted to find out. So in 1980 he decided to hold a computer tournament. He invited some of the world's leading game theorists for many different subjects to submit computer programs that would play each other. Axelrod called these programs strategies. Each strategy would face off against every other strategy and against a copy of itself and each matchup would go for 200 rounds. That's important and we'll come back to it.

Now, Axelrod used points instead of coins, but the payoffs were the same. The goal of the tournament was to win as many points as possible and in the end, the whole tournament was repeated five times over to ensure the success was robust and not just a fluke. Axelrod gave an example of a simple strategy. It would start each game by cooperating and only defect after its opponent had defected twice in a row.